My latest album was released yesterday. It’s the final release in Superpang’s digital-only series which started with Liminal Kicks (SP01) in 2020. Rushed Snares (SP200) is a follow-up, designed to end this first chapter of the label with a return to where it started, and I’m very grateful for having been given this opportunity. It’s based on the same aim of exploring sounds made with drum synths when they play very fast, so they’re heard as a pitched sound instead of a rhythm. Whereas Liminal Kicks achieved this aim by simply speeding up and slowing down exponentially, Rushed Snares uses algorithmic number sequences as the basis for the rate at which the drums play.
I found appropriate number sequences by searching the OEIS, which also provides the code to generate them. I used Mathematica to generate the sequences and transform them into MIDI files. Instead of generating drum sounds with equal volume, as in Liminal Kicks, I made them fade out within each time period by setting the volume of each hit as the inverse fraction of its position. So if a period has 2 drum hits, the first plays at full volume (1) and the second at 1/2 volume. With 3 hits, they play at 1, 2/3 and 1/3. Some of the most basic drum synths disregarded MIDI note velocity, however, so the volume fade isn’t always present in some tracks.
The basic idea was to map each number in a sequence to the number of drum hits that play in each time period. For example, the integer sequence {1, 2, 3, 4, …} played at 120bpm would have a time period of 0.5 seconds, playing 1 beat in the first period, then 2, then 3, then 4, etc. Three tracks on the album are based on this simplest of number sequences, but with different length sequences, at different speeds, with different drum synths, and one of them is reversed.
The sequences I looked for were those that didn’t just tend towards infinity but bounced around more, including smaller numbers as well as bigger ones. That way, the resulting sounds would have a range of speeds that can be heard as both rhythms and pitched tones. In addition to the basic ascending sequence of whole numbers mentioned above, I used the following integer sequences. For each sequence, I show the first 128 numbers as a list and in graph form, with an explanation of what it does and why it’s useful.
A020639
Lpf(n): least prime dividing n (when n > 1); a(1) = 1. Or, smallest prime factor of n, or smallest prime divisor of n. https://oeis.org/A020639
{1, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2, 31, 2, 3, 2, 5, 2, 37, 2, 3, 2, 41, 2, 43, 2, 3, 2, 47, 2, 7, 2, 3, 2, 53, 2, 5, 2, 3, 2, 59, 2, 61, 2, 3, 2, 5, 2, 67, 2, 3, 2, 71, 2, 73, 2, 3, 2, 7, 2, 79, 2, 3, 2, 83, 2, 5, 2, 3, 2, 89, 2, 7, 2, 3, 2, 5, 2, 97, 2, 3, 2, 101, 2, 103, 2, 3, 2, 107, 2, 109, 2, 3, 2, 113, 2, 5, 2, 3, 2, 7, 2, 11, 2, 3, 2, 5, 2, 127, 2}
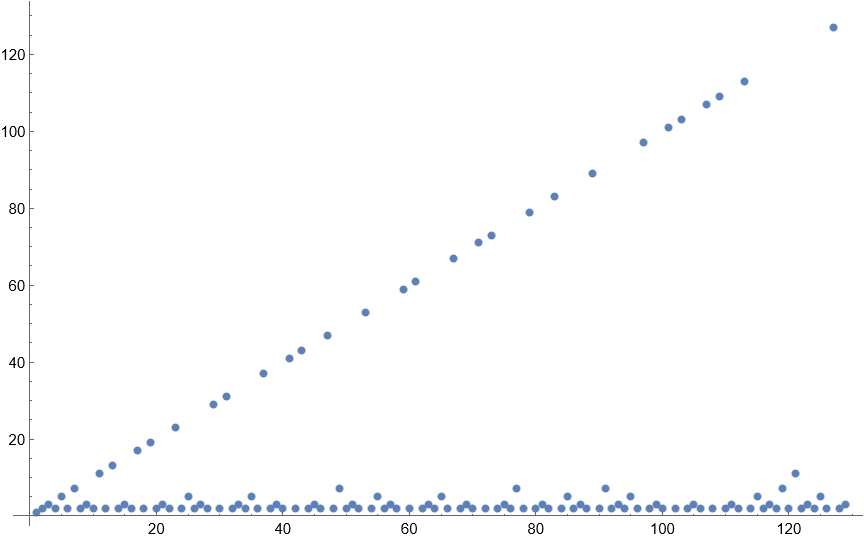
This sequence was useful for my purpose because although some elements tend towards infinity, it also includes small numbers that repeat regularly. All even-numbered elements in the sequence have the number 2, for example. The prime numbers themselves are the ones that – by definition – don’t have a lower divisor other than 1, and it’s these numbers that grow infinitely as the sequence extends, forming the diagonal line in the graph above.
A000005
d(n) (also called tau(n) or sigma_0(n)), the number of divisors of n. https://oeis.org/A000005
{1, 2, 2, 3, 2, 4, 2, 4, 3, 4, 2, 6, 2, 4, 4, 5, 2, 6, 2, 6, 4, 4, 2, 8, 3, 4, 4, 6, 2, 8, 2, 6, 4, 4, 4, 9, 2, 4, 4, 8, 2, 8, 2, 6, 6, 4, 2, 10, 3, 6, 4, 6, 2, 8, 4, 8, 4, 4, 2, 12, 2, 4, 6, 7, 4, 8, 2, 6, 4, 8, 2, 12, 2, 4, 6, 6, 4, 8, 2, 10, 5, 4, 2, 12, 4, 4, 4, 8, 2, 12, 4, 6, 4, 4, 4, 12, 2, 6, 6, 9, 2, 8, 2, 8, 8, 4, 2, 12, 2, 8, 4, 10, 2, 8, 4, 6, 6, 4, 4, 16, 3, 4, 4, 6, 4, 12, 2, 8}
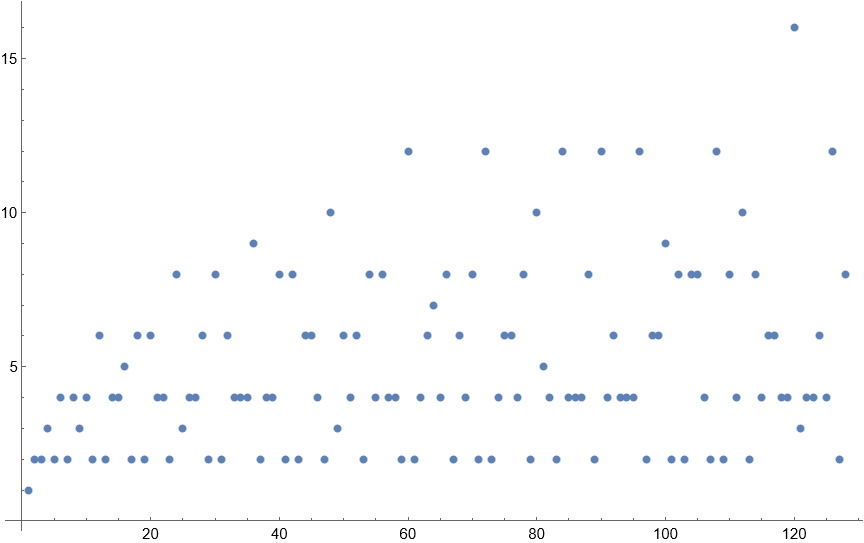
This sequence represents the number of numbers that a number can be divided into. Like the previous sequence, it grows as it expands and includes small numbers frequently. Also like the previous sequence, it has a relation to the prime numbers, but in the opposite way: Instead of the primes appearing as the largest numbers in the sequence, they are among the smallest – always (except for the first number) equalling 2, since prime numbers have only 2 divisors – 1 and themselves.
A046644
From square root of Riemann zeta function: form Dirichlet series Sum b_n/n^s whose square is zeta function; sequence gives denominator of b_n. https://oeis.org/A046644
{1, 2, 2, 8, 2, 4, 2, 16, 8, 4, 2, 16, 2, 4, 4, 128, 2, 16, 2, 16, 4, 4, 2, 32, 8, 4, 16, 16, 2, 8, 2, 256, 4, 4, 4, 64, 2, 4, 4, 32, 2, 8, 2, 16, 16, 4, 2, 256, 8, 16, 4, 16, 2, 32, 4, 32, 4, 4, 2, 32, 2, 4, 16, 1024, 4, 8, 2, 16, 4, 8, 2, 128, 2, 4, 16, 16, 4, 8, 2, 256, 128, 4, 2, 32, 4, 4, 4, 32, 2, 32, 4, 16, 4, 4, 4, 512, 2, 16, 16, 64, 2, 8, 2, 32, 8, 4, 2, 128, 2, 8, 4, 256, 2, 8, 4, 16, 16, 4, 4, 64, 8, 4, 4, 16, 16, 32, 2, 2048}
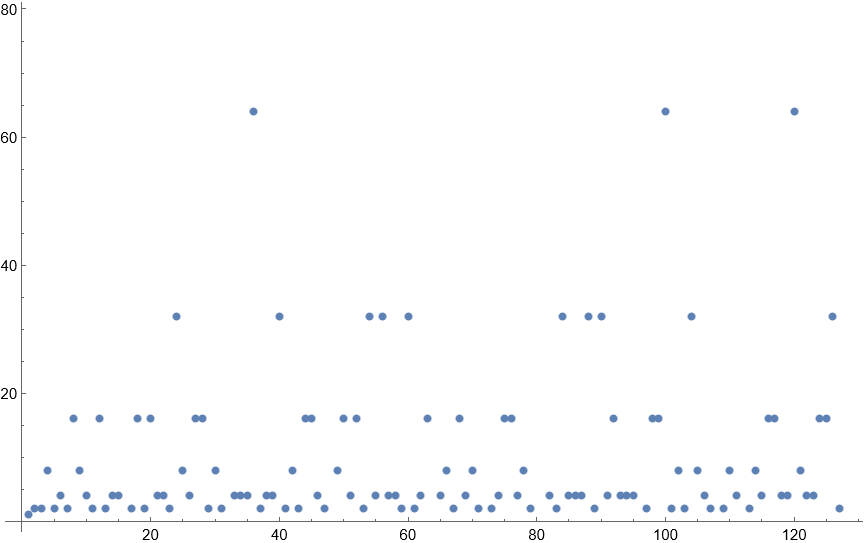
I must admit that my mathematical knowledge is insufficient to understand what’s going on in this sequence. But it has the properties that I was looking for, with a mix of small and large numbers.
A035182
Coefficients in expansion of Dirichlet series Product_p (1-(Kronecker(m,p)+1)p^(-s) + Kronecker(m,p)p^(-2s))^(-1) for m = -7. https://oeis.org/A035182
{1, 2, 0, 3, 0, 0, 1, 4, 1, 0, 2, 0, 0, 2, 0, 5, 0, 2, 0, 0, 0, 4, 2, 0, 1, 0, 0, 3, 2, 0, 0, 6, 0, 0, 0, 3, 2, 0, 0, 0, 0, 0, 2, 6, 0, 4, 0, 0, 1, 2, 0, 0, 2, 0, 0, 4, 0, 4, 0, 0, 0, 0, 1, 7, 0, 0, 2, 0, 0, 0, 2, 4, 0, 4, 0, 0, 2, 0, 2, 0, 1, 0, 0, 0, 0, 4, 0, 8, 0, 0, 0, 6, 0, 0, 0, 0, 0, 2, 2, 3, 0, 0, 0, 0, 0, 4, 2, 0, 2, 0, 0, 5, 2, 0, 0, 6, 0, 0, 0, 0, 3, 0, 0, 0, 0, 2, 2, 8}
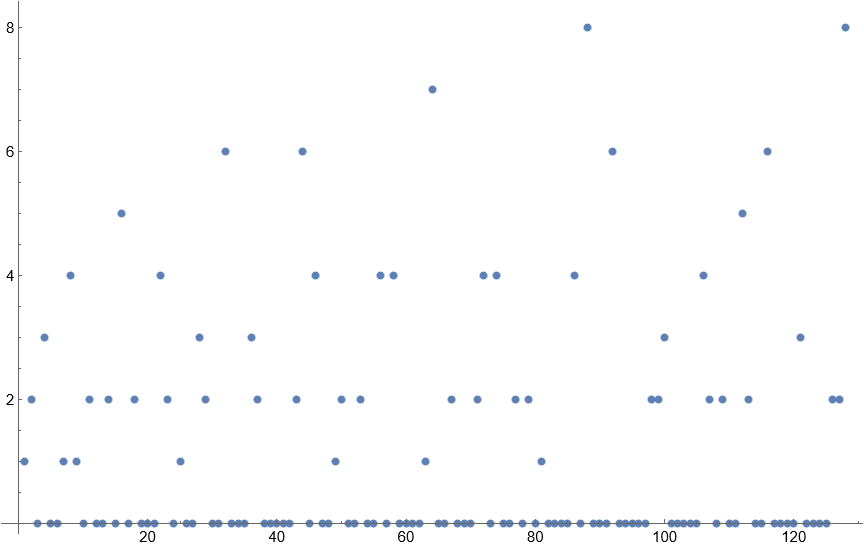
What I liked about this sequence, which is also too complicated for me to grasp, is that it includes zeroes. Dealing with zeroes instead of positive numbers required some re-writing of the code, and then it had the desired effect of leaving gaps where the zeroes are, which made a nice difference to the other sequences.
A003188
Decimal equivalent of Gray code for n. https://oeis.org/A003188
{0, 1, 3, 2, 6, 7, 5, 4, 12, 13, 15, 14, 10, 11, 9, 8, 24, 25, 27,26, 30, 31, 29, 28, 20, 21, 23, 22, 18, 19, 17, 16, 48, 49, 51, 50, 54, 55, 53, 52, 60, 61, 63, 62, 58, 59, 57, 56, 40, 41, 43, 42, 46, 47, 45, 44, 36, 37, 39, 38, 34, 35, 33, 32, 96, 97, 99, 98, 102, 103, 101, 100, 108, 109, 111, 110, 106, 107, 105, 104, 120, 121, 123, 122,126, 127, 125, 124, 116, 117, 119, 118, 114, 115, 113, 112, 80, 81, 83, 82, 86, 87, 85, 84, 92, 93, 95, 94, 90, 91, 89, 88, 72, 73, 75, 74, 78, 79, 77, 76, 68, 69, 71, 70, 66, 67, 65, 64}
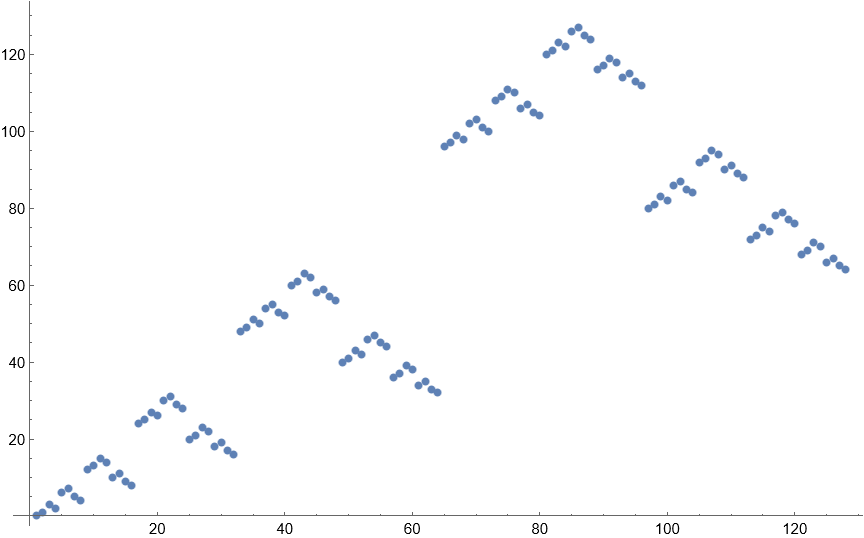
The Gray code is a sequence of binary numbers arranged such that from one number to the next only a single digit changes. This sequence represents the numbers in decimal instead of binary. What I liked about this is that it comprises all the same numbers as the simple sequence of ascending integers but in a different order. So although it too tends to infinity, it does so much less obviously. It also makes a fractal pattern when graphed, but that doesn’t translate to being able to hear it as such. It makes small groups of similar numbers with big jumps between them, making sounds that vary in pitch by both small and large amounts.

